As part of the programming languages course I’m teaching, I’ve been learning about Scala. I just used actors for the first time (after hearing a lot about them), and this post documents some of my experiences.
I’ll make the disclaimer now that I am a complete novice at Scala, so take anything I say with a grain of salt. Probably, a big grain.
Actors
In the past I’ve programmed with threads (pthreads and Java threads), message passing using PVM and MPI, and GPU computing using CUDA. I wouldn’t classify myself as an expert on parallelism and concurrency by any means, but it is something I’ve done to some reasonable degree. I’m certainly aware of the complexities of synchronizing updates to shared data, so I was intrigued by actors, and wanted to learn more about them.
The point of actors seems to be that message passing is superior to shared mutable state. Rather than having multiple threads scribble on a chunk of shared memory, you have actors (objects) that communicate with each other by sending each other messages. Sending a message to an actor is asynchronous: the message is placed in a mailbox queue, and the actor processes the message at some future time. Within a single actor, messages are processed sequentially.
Any actor that has at least one message in its queue represents a potentially-schedulable chunk of work. A pool of worker threads is given the responsibility for allowing actors with pending messages to process those messages.
Messages
Messages in Scala are objects, and actors can use pattern matching to select an action for processing each type of message they receive.
Handling a message typically involves doing some kind of processing of its contents, and then sending a result to some other actor.
Example: Mandelbrot Set
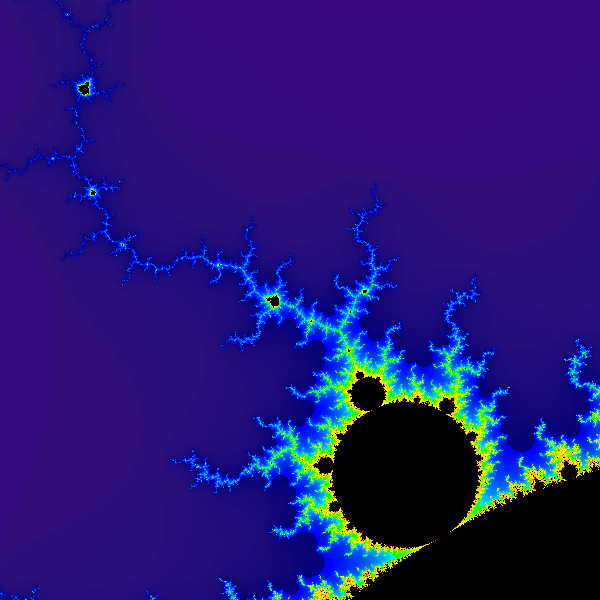
Rendering the Mandelbrot set is a good example of a trivially-parallelizable computation. Given a region of the complex plane, we decide for evenly-spaced points in that region whether each is in the Mandelbrot set. For points not in the set, we can assign a color based on how many iterations were required to prove the point is not in the set, producing a cool-looking image:
The computation for each point is independent of the computation for any other point, hence the “easy to parallelize”.
My approach to solving this problem using actors was to use a single actor to do the computation for a single row of complex numbers (sharing a common y/imaginary value). By creating one actor per row, the overall computation is parallelized at a fairly fine-grained level.
Dealing with complex numbers
To start with, we can define a Complex class to represent a complex number, using operator overloading to define multiplication and addition:
class Complex(val real : Double, val imag : Double) {
def +(other : Complex) = new Complex(real + other.real, imag + other.imag)
def *(other : Complex) = new Complex(real*other.real - imag*other.imag,
imag*other.real + real*other.imag)
def magnitude() : Double = Math.sqrt(real*real + imag*imag)
}Doing the actual (sequential) computation
Next, a Row class to represent one row of the computation. The compute method computes an iteration count for each complex number in one row:
object Row {
val THRESHOLD = 1000
}
class Row(val xMin : Double, val xDiff : Double, val y : Double, val row : Int,
val numPoints : Int) {
def compute() : List[Int] = {
(0 until numPoints).map( i => {
val C = new Complex(xMin + i*xDiff, y)
var Z = new Complex(0.0, 0.0)
var count = 0
while (Z.magnitude() < 2.0 && count < Row.THRESHOLD) {
Z = Z*Z + C
count = count + 1
}
count
}).toList
}
}You’ll note that I’m doing the computation for each complex number using a loop which modifies the values of variables. I guess I should be trying to stick to a functional style, although I think being able to mix mix functional and imperative styles is a significant strength of Scala. Perhaps someone could enlighten me on when it would make sense to prefer one style over the other.
Adding some actors!
Now, for the important bit: the RowActor class. RowActors are actors that compute the iteration counts for one row:
import scala.actors.Actor
class RowActor extends Actor {
def act() = {
loop {
react {
case row : Row => {
sender ! (row.rowNum, row.compute())
exit()
}
}
}
}
}Each actor class must define an act method, which specifies how the actor will react to messages it receives. I won’t even pretend that I can explain precisely what the loop and react functions are (there is some sort of magic going on involving partial functions, I think). The basic idea is that loop causes the actor to process all of the messages it receives, and react is a construct for pattern matching on received messages. In the case of RowActor, it handles Row messages by calling compute, and then sending a pair containing the row number and the computed iteration count list back to the sender (the actor that sent the message). At that point, the RowActor does not need to do any further work, so it calls exit to shut itself down.
Running the show
The Mandelbrot class is an actor that coordinates the overall computation. It is given the boundaries of the region of the complex plane in which to do the computation, and given the number of rows and columns of iteration counts to generate. When it receives a Get message, it creates RowActors to compute each row, and waits to receive their completed iteration count lists. When it has received all completed rows, it sorts them by row number and sends the sorted list back to the actor that sent the original Get message:
import scala.actors.Actor
import scala.actors.Actor._
import scala.actors.OutputChannel
case object Get
class Mandelbrot(x1 : Double, y1 : Double,
x2 : Double, y2 : Double,
nCols : Int, nRows : Int) extends Actor {
var resultSink : OutputChannel[Any] = null
var partialResults : List[(Int, List[Int])] = List()
var rowsReceived : Int = 0
def act() = {
loop {
react {
case Get => {
// Make a note of which actor requested the results of the computation
resultSink = sender
// Start RowActors to compute each row
for (j <- 0 until nRows) {
val xDiff = (x2 - x1) / nCols
val yDiff = (y2 - y1) / nRows
val row = new Row(x1, xDiff, y1 + j*yDiff, j, nCols)
val rowActor = new RowActor()
rowActor.start()
rowActor ! row
}
}
case r : (Int, List[Int]) => {
// A RowActor is sending us completed results for a row
partialResults = r :: partialResults
rowsReceived += 1
// Are all rows finished?
if (rowsReceived == nRows) {
// Sort rows by row number (since they probably arrived out of order)
val results = partialResults.sortWith( (l, r) => l._1 < r._1 )
// Send sorted results to the actor that requested them
resultSink ! results
// Computation is done
exit()
}
}
}
}
}
}The Mandelbrot actor does contain mutable data. However, the way it is used is safe because each message is processed sequentially.
There is probably a more elegant way to specify that the completed results should be sent back to the actor which sent the initial Get message: I’m saving a reference to its OutputChannel in a mutable field.
Getting the results: not as easy as you might think
The last bit is to create the Mandelbrot actor, send it a Get message, and wait for the results to come back. Interestingly, waiting for an asynchronous actor-based computation to finish is not particularly straightforward in Scala, and I did not find any tutorials on actors that explained how to do this. Actors can certainly send messages to other actors, so you can ship your result to any actor. But, presumably there was some code that created the actors, which is not itself an actor! How do we get the result of the computation back to that code?
Fortunately for me, I happen to know Chris League, who sent me a link to a talk he gave about actors in Scala. It turns out there is a !! operator which sends a message to an actor and returns a future which, if applied, waits for a reply back from that actor. That is why the Mandelbrot actor keeps track of the sender of the original Get message: that is the actor to which the final result will be delivered, although thanks to !! it’s a special actor that can communicate back to the non-actor code that started the computation. (I’m not sure precisely how this works behind the scenes.)
One minor issue is that the future’s type does not specify what type of message will be sent back (since that is unknowable). However, we can easily pattern match on the result to convert it to the type we expect:
object Main {
val ROWS = 10
val COLS = 10
val x1 = -2.0
val y1 = -2.0
val x2 = 2.0
val y2 = 2.0
def main(args: Array[String]) {
val m = new Mandelbrot(x1, y1, x2, y2, COLS, ROWS)
m.start()
val f = m !! Get
val untypedResults = f()
untypedResults match {
case results : List[(Int, List[Int])] => {
results.foreach( pair => {
println(pair._1 + ": " + pair._2)
})
}
}
}
}This produces the following output:
0: List(1, 1, 1, 1, 1, 1, 1, 1, 1, 1)
1: List(1, 1, 1, 2, 2, 2, 2, 2, 1, 1)
2: List(1, 1, 2, 3, 3, 3, 2, 2, 2, 1)
3: List(1, 3, 3, 4, 6, 18, 4, 2, 2, 2)
4: List(1, 3, 7, 7, 1000, 1000, 9, 3, 2, 2)
5: List(1, 1000, 1000, 1000, 1000, 1000, 7, 3, 2, 2)
6: List(1, 3, 7, 7, 1000, 1000, 9, 3, 2, 2)
7: List(1, 3, 3, 4, 6, 18, 4, 2, 2, 2)
8: List(1, 1, 2, 3, 3, 3, 2, 2, 2, 1)
9: List(1, 1, 1, 2, 2, 2, 2, 2, 1, 1)
Yup, that’s the Mandelbrot set! Maybe not the prettiest rendering of it, but not bad for a proof of concept.
Eye candy
Scala runs on the JVM. So, we can always use standard Java classes and methods if we need to, including BufferedImage and ImageIO:
import java.awt.image.BufferedImage
import java.awt.Color
import javax.imageio.ImageIO
import java.io.FileOutputStream
class ImageRenderer {
def render(results : List[(Int, List[Int])], nCols : Int, nRows : Int,
fileName : String) = {
val img = new BufferedImage(nCols, nRows, BufferedImage.TYPE_INT_ARGB)
val g = img.getGraphics()
results.foreach( pair => {
pair._2.zipWithIndex.foreach {
case (count, i) => {
val color =
if (count < 1000) {
val intensity = ((Math.log(count) / Math.log(1000)) * 255).toInt
new Color(0, intensity, 255-intensity)
} else
Color.BLACK
g.setColor(color)
g.fillRect(i, pair._1, 1, 1)
}
}
})
val os = new FileOutputStream(fileName)
ImageIO.write(img, "PNG", os)
os.close()
}
}Adjusting our main function to render an image, increasing ROWS and COLS to 600x600, and changing the region boundaries to match the image above, and we get this:
Not the most interesting choice of colors, but hey, what do you expect in 5 minutes?
All of the code described above is in a git repository:
https://github.com/daveho/ScalaActors
What I learned
I think I learned enough about actors that I could comfortably apply them to other kinds of problems. I’m not sure if I really used actors the right way in the Mandelbrot code above, but my whole life has been dedicated to doing things the wrong way, so that’s to be expected.
I definitely feel like I’ve gotten over the initial hump with Scala: I know enough to do basic things, and the internet (especially StackOverflow) has enough examples of how to do other things in Scala that I can make progress. I’m sure it will take significant further study to get a handle on Scala’s type system. I should probably sit down and read a good book on Scala. (Recommendations?)
I definitely like the fact that Scala has an escape hatch: I can revert to doing things in an imperative/Java style. Meaningful change is usually incremental. I don’t think the functional programming revolution is going to occur by having everyone renounce side effects all at once. However, I can see getting there a little bit at a time, or maybe learning to be functional enough to get the benefits but still cheat when it’s expedient to do so.
blog comments powered by Disqus